함수 요약
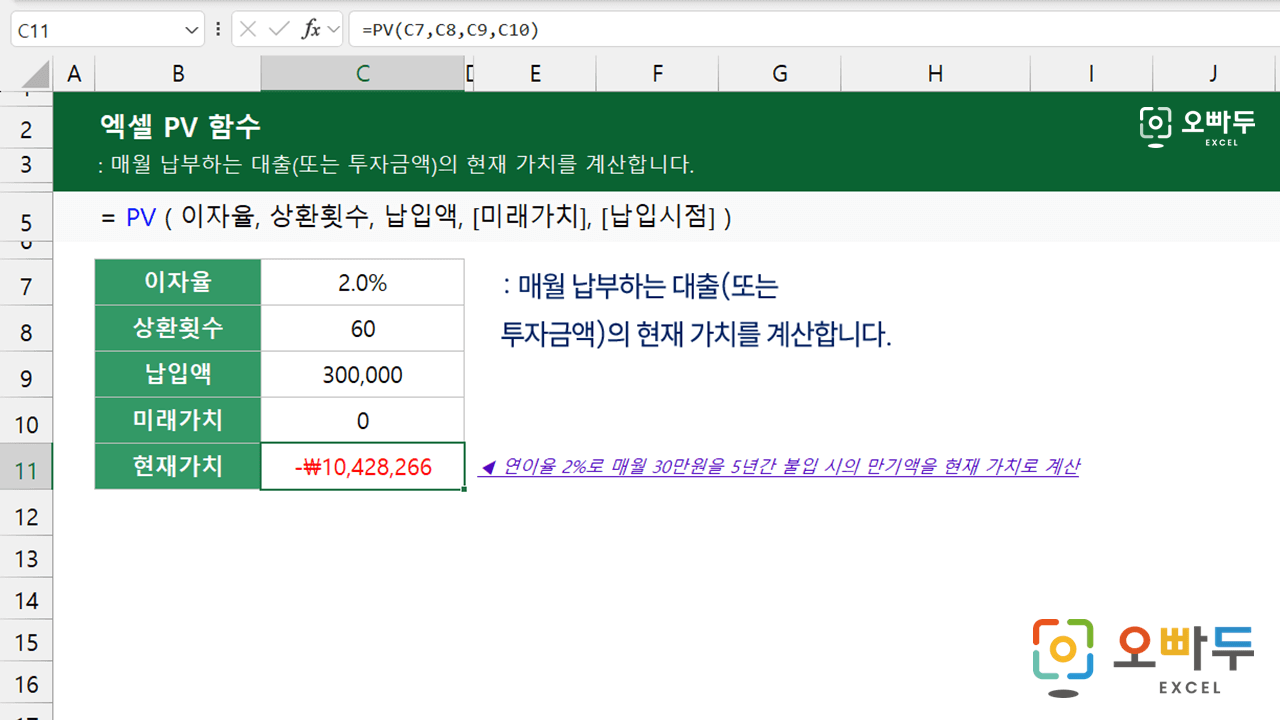
엑셀 PV 함수는 고정금리로 매월 납부하는 대출(또는 투자금액)의 현재 가치를 계산하는 함수입니다.
👉 PV함수는 단리가 아닌 복리로 계산하는 것에 주의합니다.
함수 구문
=PV(이자율, 상환횟수, 납입액, [미래가치], [납입시점])
•
이자율
-
각 기간의 이자율입니다.
- 연 이자율을 사용할 경우 12로 나누어 월 이자율로 계산합니다.
•
상환횟수
-
대출금(또는 적금)의 총 납입 횟수 입니다.
- 예를 들어, 3년 월납의 경우 3*12 = 36이 됩니다.
•
납입액
-
각 기간에 납입하는 금액입니다.
•
미래가치
-
[선택인수]납입 완료 후 남게 될 잔액입니다. 기본값은 0입니다.
•
납입시점
-
[선택인수]납입이 이루어지는 시점입니다. 기본값은 기간말입니다.
- 0 : [기본값] 기간말
- 1 : 기간초
상세 설명
엑셀 PV 함수는 고정금리로 매월 납부하는 대출(또는 투자액)의 현재 가치를 계산하는 함수입니다. 예를 들어, 매월 일정액을 적금하거나 대출금을 상환할 때 전체 금액에 대한 현재 시점 가치를 계산할 수 있습니다. 이 함수는 정기적인 납입과 고정된 이자율에서 '복리'를 기준으로 계산합니다.
=PV(2.5%,10,100000000) / / 매년 2.5%의 물가 상승률을 가정했을 때, 10년뒤 1억원의 현재 가치를 계산합니다.
PV 함수는 기타 세금 및 수수료를 결과값에 반영하지 않습니다. 현재가치가 아닌 미래가치를 계산하려면 FV 함수를 사용하세요.
PV 함수 간단 예제
1) 물가상승률 고려시, n년 후 돈의 가치
물가 상승률 2%를 고려 시, 1년 후 100만원의 가치는 다음과 같이 구할 수 있습니다.
=PV(2%,1,,1000000) / / 결과 : 980,392원
2) 물가상승률을 고려한 현재 가치 계산
매년 2%의 물가 상승률로 10년 뒤 1억원의 현재 가치는 다음과 같이 구할 수 있습니다.
=PV(2%,10,100000000) / / 결과 : 898,258,500 / / → 2% 물가상승률로 10년뒤 1억원은 현재 가치로 8,982만원으로 계산 가능
3) 월납 적금의 현재 가치 계산
연이율 4%로 15년간 매월 20만원을 납입하는 적금의 현재 가치는 다음과 같이 계산할 수 있습니다.
=PV(4%/12, 15*12, -200000) / / 결과 : 27,038,430 / / → 연이율 4%의 20만원 적금을 15년간 만기 시, 현재 가치는 약 2천 7백만원입니다.
그 외 주의사항
이자율은 상환 횟수의 기간과 동일한 단위로 입력합니다. 만약 상환 기관이 12개월이라면, 이율도 연이율 2.4%/12(=0.2%)로 입력합니다.
PV 함수는 이자율을 복리로 적용하는 것을 주의합니다. (대부분의 시중은행은 금리를 단리로 적용합니다.)
기타 세금 및 수수료등 부가 요인은 PV 함수 결과에 반영되지 않으므로 별도로 고려해야 합니다.
MS 공식 홈페이지 링크
댓글 1
로그인 후 댓글을 작성할 수 있습니다.
강민준🤗
2024.08.11 07:50
좋은 강의 감사합니다🙇♂️